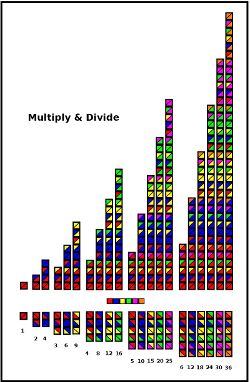
In Multiply and Divide the blocks are diagonally divided (two bits per block) and numbered with maximum base 6.
In the lower section, the blocks are simply laid out (from one block of one -up to 6 blocks of 6) and numbered sequentially.
In the upper section, the blocks are piled up on each other -culminating in n ^ 2 (maximum 6 x 6 = 36)
Add and Subtract:

Add and Subtract are basically "partitions"
(all the smaller numbers that a lager number can be broken down to make the sum of the original number)
Usually 6,1 is considered the same a 1, 6 (when partioning 7, for example)
-but in these drawings they are considered different.
The method used to generate the partitions also affect the pattern created when all are combined -but more of this later.....
Partition 1:
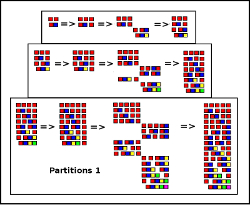
One way of generating partitions is to take the previous set and add one to each of the previous partitions
The new set will then need to be slightly "re-partitioned" to fill in the missing patterns
Partition 2:
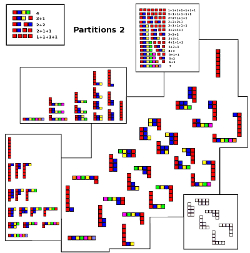
The Basic Set of Partitions with no repetitions (i.e. 6,1 is considered the same a 1,6)
can be represented by images that look like a bunch of Tally Sticks next to each other
When rotated, the images can represent a different combination of Partitions.
This drawing suggests some of the possibilities
Partition 3:
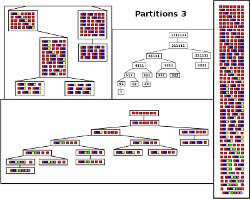
The Basic Partition Set can be represented in a Tree Diagram
(showing the transition from one partition to another)
The Extended Set (with repetitions) is created by permutation of the elements of the Basic Set
Partition 4:
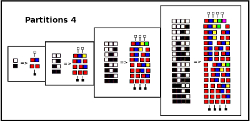
An elegant way to generate the Extended Set -is to count the potential Segmentation Points
(Cutting Places)
These Segmentation Points can then be binary coded (a cut = 1, a non-cut = 0)
-and one simply enumerates (counts) all the binary numbers with the same number of digits as cutting points