Naming Variables:
Each Dimension in the Parametrical Space system is composed of three
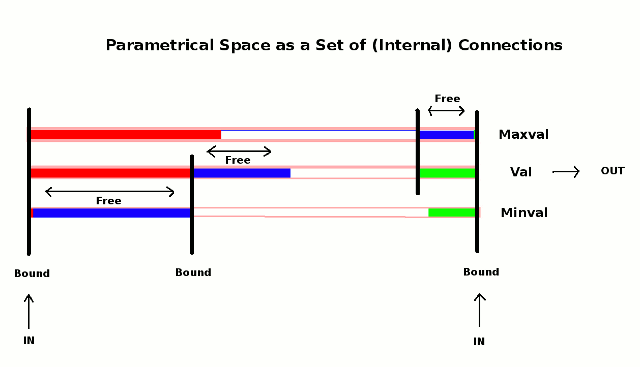
linked Parameters {Maxval, Val, Minval}
Each Parameter has four main variables {min, max, pos, inc}
min -> is the (current) minumum permitted
max -> is the current maximum permitted
pos -> is the current value (between min and max)
inc -> is the increment which is added (or subtracted) to the current pos to get the next pos
Minval.min and Maxval.max represent the absolute (fixed) limits of the system and are fixed during the initialisation process
Val.pos represents the output of the system
Minval.inc, Maxval.inc and Val.inc are all inputs -and can be changed via the control interface
Each Parameter has four main variables {min, max, pos, inc}
min -> is the (current) minumum permitted
max -> is the current maximum permitted
pos -> is the current value (between min and max)
inc -> is the increment which is added (or subtracted) to the current pos to get the next pos
Minval.min and Maxval.max represent the absolute (fixed) limits of the system and are fixed during the initialisation process
Val.pos represents the output of the system
Minval.inc, Maxval.inc and Val.inc are all inputs -and can be changed via the control interface
Describing the Connections:
Val is the main parameter. Minval and Maxval control the
temporary minimum and
maximum values of Val.
if (depending on the control settings) Val.pos equals or exceeds its current minimum or maximum value, then the opposing limit is changed. i.e. if Val.pos reaches Val.max, then Val.min is changed.
Val.min and Val.max are linked to respectively Minval.pos and Maxval.pos,
So, for example, Val.min is changed by adding (or subtracting) Minval.inc to the current value of Minval.pos -and after testing and possible correction to ensure that it is within its own limits, Val.min is set to the current value of Minval.pos.
A similar proceedure modifies Val.max.
if (depending on the control settings) Val.pos equals or exceeds its current minimum or maximum value, then the opposing limit is changed. i.e. if Val.pos reaches Val.max, then Val.min is changed.
Val.min and Val.max are linked to respectively Minval.pos and Maxval.pos,
So, for example, Val.min is changed by adding (or subtracting) Minval.inc to the current value of Minval.pos -and after testing and possible correction to ensure that it is within its own limits, Val.min is set to the current value of Minval.pos.
A similar proceedure modifies Val.max.
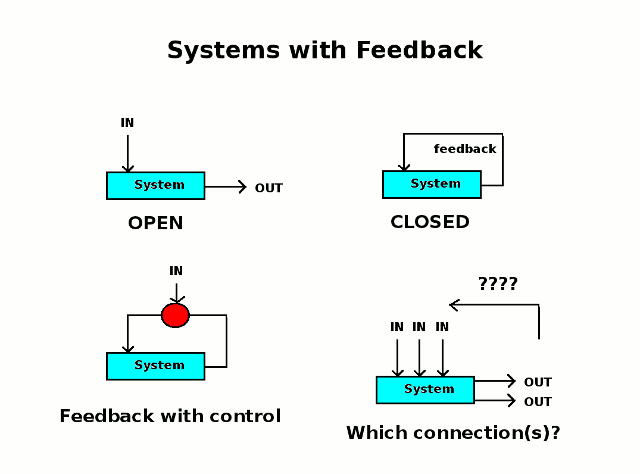
Feedback:
In a system with input and
output variables -it is theoretically possible to connect output and input (internally or
externally) so that what comes out can be fed back in.
If more than one input or output is available, then the question is raised of which input should be conmnected to which output.
If more than one input or output is available, then the question is raised of which input should be conmnected to which output.
Control:
The connection between output and input can be modified or
unmodified.
In some cases, it may be advisable to add a modifier that will allow the level of feedback to be regulated.
Feedback can increase or decrease the stability of the system.
Positive feedback amplifies the current behaviour of the system because it increases as output levels increase and decreases if output levels decrease.
Negative feedback inverts the output and so contributes to system stability.
Obviously, an open system that would become closed by the feedback loop becomes open again if the feedback level is subject to external control -because system behaviour is now modified via this external control, instead of the original input level.
In some cases, it may be advisable to add a modifier that will allow the level of feedback to be regulated.
Feedback can increase or decrease the stability of the system.
Positive feedback amplifies the current behaviour of the system because it increases as output levels increase and decreases if output levels decrease.
Negative feedback inverts the output and so contributes to system stability.
Obviously, an open system that would become closed by the feedback loop becomes open again if the feedback level is subject to external control -because system behaviour is now modified via this external control, instead of the original input level.
Open and Closed:
A system which has inputs and outputs is an open system
A system that has no inputs (but possibly outputs -or it would be invisible) is called a closed system
In practice it may be difficult to decide if a system is completely open or completely closed.
This may also depend on who is using the system: For example, the owner may be able to access controls which the normal user cannot. In which case, the system would appear to be open to the owner and closed to the user.
A system that has no inputs (but possibly outputs -or it would be invisible) is called a closed system
In practice it may be difficult to decide if a system is completely open or completely closed.
This may also depend on who is using the system: For example, the owner may be able to access controls which the normal user cannot. In which case, the system would appear to be open to the owner and closed to the user.